Home > Topdrawer > Geometric reasoning > Big ideas > Plane shapes > Polygons
Polygons
A polygon is a closed plane figure bounded by a finite number of line segments. Very often we are concerned with simple polygons, where the boundary does not cross itself.
Polygons are usually named according to the number of sides they possess. For example, a three-sided polygon is a triangle, four-sided a quadrilateral, five-sided a pentagon. You can download the Naming polygons: Information sheet.
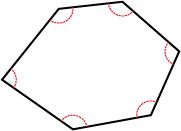
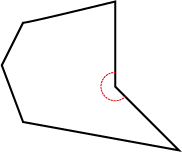
Polygons are either convex or non-convex. In a convex polygon all of the angles are less than 180 degrees. A non-convex polygon must have at least one interior angle greater than 180 degrees. This is called a reflex angle. You can download a Convex and non-convex polygons: Information sheet.
A convex polygon. |
A non-convex polygon. |
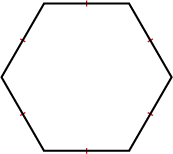
Polygons are either regular or irregular. Regular polygons have all sides and all angles equal. You can download a Regular and irregular polygons: Information sheet.
A regular hexagon. |
An irregular hexagon.
|
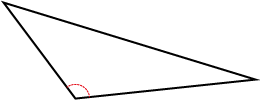
Triangles are classified according to their sides and their angles. The triangle below is called an obtuse-angled scalene triangle because one angle is greater than 90° (obtuse) and its sides are different lengths (scalene). You can download the Classifying triangles: Information sheet.
Obtuse-angled scalene triangle.
Quadrilaterals are classified using their properties. There are six special quadrilaterals identified in the Australian Curriculum: squares, rectangles, parallelograms, rhombuses, trapeziums and kites. You can download a Special quadrilaterals: Information sheet. You can also download the Properties of quadrilaterals: Information sheets showing the properties for each of the six quadrilaterals.
